63. Unique Paths II
A robot is located at the top-left corner of a m x n grid (marked 'Start' in the diagram below).
The robot can only move either down or right at any point in time. The robot is trying to reach the bottom-right corner of the grid (marked 'Finish' in the diagram below).
Now consider if some obstacles are added to the grids. How many unique paths would there be?
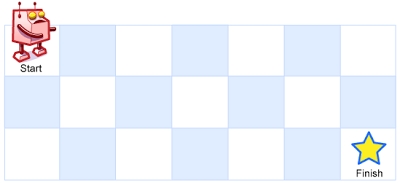
Example:
解法
动态规划
引用
Last updated
Was this helpful?