62. Unique Paths

描述

A robot is located at the top-left corner of a m x n grid (marked 'Start' in the diagram below).

The robot can only move either down or right at any point in time. The robot is trying to reach the bottom-right corner of the grid (marked 'Finish' in the diagram below).

How many possible unique paths are there?

例图

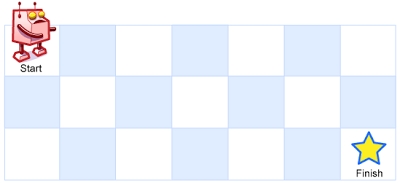
Example 1:

Input: m = 3, n = 2
Output: 3
Explanation:
From the top-left corner, there are a total of 3 ways to reach the bottom-right corner:
1. Right -> Right -> Down
2. Right -> Down -> Right
3. Down -> Right -> Right

Example 2:

Input: m = 7, n = 3
Output: 28

解法

动态规划

class Solution:
    def uniquePaths(self, m: int, n: int) -> int:
        # dp[i][j] how many ways from dp[0][0] to dp[i][j]
        dp = [[0 for _ in range(m)] for _ in range(n)]

        # can only move to right, so all the dp[0][..] is 1
        for i in range(m):
            dp[0][i] = 1

        # can only move to down, so all the dp[j][0] is 1
        for j in range(n):
            dp[j][0] = 1

        # dp[i][j] = dp[i-1][j] + dp[i][j-1]
        for i in range(1, n):
            for j in range(1, m):
                dp[i][j] = dp[i-1][j] + dp[i][j-1]

        return dp[-1][-1]

组合数

7 * 3 的方格中从左上角走到右下角一共 8 步，其中选 2 步向下，其余向右，一共 $C_{8}^{2}$ 种选法。推广到 m * n 有，$C_{m+n-2}^{m-1}$。

引用